
29. Februar 2024
Qualitätswerkzeuge Part 5: Das Streudiagramm als empirisch gestütztes und einfaches Analysetool für Qualitätsbeauftragte
Standen Sie schon einmal vor der Herausforderung, Wechselwirkungen zwischen Prozessvariablen in Ihrem Unternehmen identifizieren zu müssen? Blieb zum Beispiel das Endprodukt trotz hochwertiger Rohstoffe immer wieder hinter den Qualitätsanforderungen zurück? Stand die Frage des „Warum“ im Raum? Diese Gemengelage – ob nur theoretisch angenommen oder sogar praktisch erlebt – kann ein Hinweis darauf sein, dass die komplexen Beziehungen zwischen den Prozessvariablen, hier in dem Fall Rohstoffqualität und Maschineneinstellungen, nicht ideal aufeinander abgestimmt waren. Um der Sache dann jedoch richtig auf die Spur zu kommen, gilt es, in einem ersten Schritt zu verstehen, ob überhaupt Zusammenhänge bestehen und wenn ja, welcher Art und Stärke diese sind.
Part 5 unserer Reihe Qualitätswerkzeuge effektiv einsetzen richtet dafür das Augenmerk auf ein elementares Instrument der Datenanalyse, was für die Lösung der gerade beschriebenen Situation zur Anwendung kommt: Streu- bzw. Korrelationsdiagramme, die die linearen Beziehungen zwischen zwei Variablen einfach visuell darstellen. So können Sie die Korrelation zwischen unterschiedlichen Datensätzen analysieren und interpretieren, was in der Folge eine präzise Einschätzung der Prozessperformance ermöglicht.
Lesezeit: 4 Minuten
Um die Ergebnisse des Streu- bzw. Korrelationsdiagramms auch wirklich sinnvoll interpretieren zu können, ist es wichtig, sich bereits vor der Erstellung mit dem Prinzip von Korrelationen auseinanderzusetzen. Eine Korrelation zeigt Zusammenhänge zwischen zwei oder mehr Variablen auf. Diese Zusammenhänge können positiv oder negativ sein. Ein einfaches Beispiel für eine positive Korrelation ist, dass der Verkauf von Sonnenschutzprodukten mit steigenden Temperaturen zunimmt. Eine negative Korrelation zeigt sich hingegen beim Verkauf von Heizgeräten, der in wärmeren Monaten eher abnimmt.
Doch nun zur praktischen Anwendung: Streudiagramme machen die beschriebenen Korrelationen auf einen Blick sichtbar. Die auf Basis der Darstellung nachfolgende Korrelationsanalyse identifiziert entsprechende Zusammenhänge.
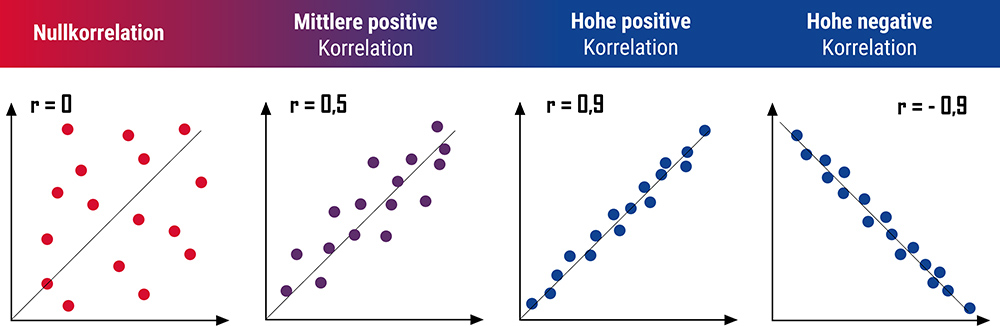
Abbildung 1: Darstellung verschiedener Zusammenhänge und ihrer Stärke
Eine grundlegende Voraussetzung für die Durchführung einer Korrelationsanalyse ist das Vorliegen von metrischen quantitativen Daten. Solche Daten sind Werte wie Anzahl/Menge/Stück, Gewicht, Temperatur oder Volumen, aber auch Einkommen, Gewinn, Umsatz u.ä. Zur Veranschaulichung lässt sich da zum Beispiel an die Beziehung zwischen der Anzahl der in einem Haushalt lebenden Personen und dem Wasserverbrauch denken. Mit jeder Person mehr steigt auch die benötigte Wassermenge. Etwas komplizierter, aber immer noch darstellbar wäre die Abhängigkeit des Energieverbrauchs eines Hauses von der Außentemperatur, wobei hier die weiter oben genannte Einlassung zum Messbereich beachtet werden sollte. Den zu betrachtenden „Nullpunkt“ würde man auf 20°C festlegen, einem Temperaturbereich, bei dem weder geheizt noch gekühlt werden müsste. Steigt jedoch der Wert Temperatur wesentlich an, erhöht sich der Wert Energieverbrauch für die Kühlung, was wie weiter oben ausgeführt eine positive Korrelation darstellt. Ebenso wäre das Absinken des Wertes Temperatur mit einer stetigen Erhöhung des Wertes Energieverbrauch, diesmal für die Heizung, verbunden, auch hier übrigens eine positive Korrelation. In jedem Fall lassen die Relationen und Abstände zwischen den Werten der Variablen eine sinnvolle Interpretation zu.
Im Gegensatz dazu kann mit nicht-metrischen Daten keine Korrelationsanalyse durchgeführt werden. Dazu zählen kategoriale Daten, wie zum Beispiel die Farbe eines Autos. Möchte man herausfinden, ob die Autofarbe seine Verkaufszahlen beeinflusst, müsste man die Farben in eine metrische Variable überführen, d.h. jeder Farbe Zahlen zuweisen. Dies ist bei der Interpretation mitunter kompliziert - zumal anzunehmen ist, dass nicht unbedingt ein linearer Zusammenhang besteht (s. Abbildung 2). Die Farbe stellt also zunächst eine Gruppeneinteilung dar, ohne dass diese Gruppen auf einer numerischen Skala angeordnet sind.

Abbildung 2: Fiktives Beispiel. Es zeigt sich, dass je nach Autofarbe unterschiedlich viele Autos verkauft werden. Allerdings lässt sich in diesem Fall - selbst bei Zuweisung zu Nummern zu den Farben - kein korrelativer Zusammenhang ableiten.
Wie eben bereits erwähnt, sind nicht-lineare Beziehungen in der Korrelationsanalyse problematisch. Angenommen, es besteht eine kurvilineare (krummlinig, gekrümmt) Beziehung zwischen der Arbeitszufriedenheit und der Anzahl an Weiterbildungen: Bis zu einem gewissen Punkt führt eine höhere Anzahl an Weiterbildungen zu einer gesteigerten Arbeitszufriedenheit. Ab einem bestimmten Punkt sind die Mitarbeiter aber von der Anzahl der Weiterbildungen überfordert oder schaffen ihre tägliche Arbeit nicht mehr, wodurch ihre Zufriedenheit sinkt (s. Abbildung 3). Eine Korrelationsanalyse könnte fälschlicherweise eine schwache oder gar keine Beziehung anzeigen, obwohl tatsächlich ein signifikanter Effekt vorliegt.

Abbildung 3: Fiktives Beispiel. Es besteht ein kurvilinearer Zusammenhang zwischen der Anzahl der Weiterbildung und der Arbeitszufriedenheit (grün Linie). Der lineare Korrelationskoeffizient (rote Linie) zeigt allerdings keinen Zusammenhang an.
Darüber hinaus können sog. Ausreißer die Analyse verzerren, da sie den Koeffizienten künstlich erhöhen oder senken können. Solche Ausreißer müssen also vor der Analyse identifiziert und ggf. ausgeschlossen werden.
Part 5 unserer Reihe Qualitätswerkzeuge effektiv einsetzen richtet dafür das Augenmerk auf ein elementares Instrument der Datenanalyse, was für die Lösung der gerade beschriebenen Situation zur Anwendung kommt: Streu- bzw. Korrelationsdiagramme, die die linearen Beziehungen zwischen zwei Variablen einfach visuell darstellen. So können Sie die Korrelation zwischen unterschiedlichen Datensätzen analysieren und interpretieren, was in der Folge eine präzise Einschätzung der Prozessperformance ermöglicht.
Lesezeit: 4 Minuten
Um die Ergebnisse des Streu- bzw. Korrelationsdiagramms auch wirklich sinnvoll interpretieren zu können, ist es wichtig, sich bereits vor der Erstellung mit dem Prinzip von Korrelationen auseinanderzusetzen. Eine Korrelation zeigt Zusammenhänge zwischen zwei oder mehr Variablen auf. Diese Zusammenhänge können positiv oder negativ sein. Ein einfaches Beispiel für eine positive Korrelation ist, dass der Verkauf von Sonnenschutzprodukten mit steigenden Temperaturen zunimmt. Eine negative Korrelation zeigt sich hingegen beim Verkauf von Heizgeräten, der in wärmeren Monaten eher abnimmt.
Bestimmt werden Korrelationen mit dem Korrelationskoeffizienten r, der Werte zwischen +1 und -1 annehmen kann (s. Abbildung 1). Ein Wert von +1 bedeutet dabei, dass die Korrelation perfekt positiv ist. Wenn die eine Variable zunimmt, steigt auch die andere Variable im gleichen Verhältnis linear an. Je geringer der Wert, umso geringer ist der Zusammenhang. Das gleiche Bild zeigt sich bei einer negativen Korrelation: Ein Korrelationskoeffizient unterhalb r = 0 bedeutet, dass die Korrelation negativ ist, d.h. wenn eine Variable zunimmt, nimmt die andere Variable linear ab. Je näher der Koeffizient bei -1 liegt, umso stärker ist der Zusammenhang. Bei einer sog. Nullkorrelation (r = 0) besteht kein offensichtlicher linearer Zusammenhang zwischen den Variablen. Wichtig: Dennoch ist es möglich, dass durchaus eine „verdeckte“ Korrelation zwischen den beiden Variablen besteht, entweder, weil die Abhängigkeit im nichtlinearen Bereich liegt oder aber der Messbereich mindestens einer der Variablen nicht richtig gewählt ist. So wird beispielsweise das Ansteigen der Tagestemperaturen von 0 auf 15°C noch nicht zu erhöhtem Sonnencremebedarf führen, sehr wohl aber, wenn sich die durchschnittlichen Temperaturen von 15 in Richtung 30°C bewegen. Was das Beispiel übrigens noch zeigt, ist eine oft bestehende Abhängigkeit zu weiteren Variablen, wie in diesem Fall zur Anzahl der Sonnenstunden – denn kaum jemand benutzt Sonnencreme, wenn es draußen zwar 30 °C heiß, aber der Himmel völlig bedeckt ist. Alles in allem Hinweise, dass einerseits Streu- bzw. Korrelationsdiagramme sehr schnell und pragmatisch Aussagen liefern können, mit denen man dann weiterarbeiten kann, andererseits ihr Einsatz jedoch immer mit Augenmaß erfolgen sollte, um nicht unbemerkt falsche Rückschlüsse zu ziehen.
Doch nun zur praktischen Anwendung: Streudiagramme machen die beschriebenen Korrelationen auf einen Blick sichtbar. Die auf Basis der Darstellung nachfolgende Korrelationsanalyse identifiziert entsprechende Zusammenhänge.

Abbildung 1: Darstellung verschiedener Zusammenhänge und ihrer Stärke
Voraussetzungen für eine Korrelationsanalyse
Im Gegensatz dazu kann mit nicht-metrischen Daten keine Korrelationsanalyse durchgeführt werden. Dazu zählen kategoriale Daten, wie zum Beispiel die Farbe eines Autos. Möchte man herausfinden, ob die Autofarbe seine Verkaufszahlen beeinflusst, müsste man die Farben in eine metrische Variable überführen, d.h. jeder Farbe Zahlen zuweisen. Dies ist bei der Interpretation mitunter kompliziert - zumal anzunehmen ist, dass nicht unbedingt ein linearer Zusammenhang besteht (s. Abbildung 2). Die Farbe stellt also zunächst eine Gruppeneinteilung dar, ohne dass diese Gruppen auf einer numerischen Skala angeordnet sind.

Abbildung 2: Fiktives Beispiel. Es zeigt sich, dass je nach Autofarbe unterschiedlich viele Autos verkauft werden. Allerdings lässt sich in diesem Fall - selbst bei Zuweisung zu Nummern zu den Farben - kein korrelativer Zusammenhang ableiten.
Wie eben bereits erwähnt, sind nicht-lineare Beziehungen in der Korrelationsanalyse problematisch. Angenommen, es besteht eine kurvilineare (krummlinig, gekrümmt) Beziehung zwischen der Arbeitszufriedenheit und der Anzahl an Weiterbildungen: Bis zu einem gewissen Punkt führt eine höhere Anzahl an Weiterbildungen zu einer gesteigerten Arbeitszufriedenheit. Ab einem bestimmten Punkt sind die Mitarbeiter aber von der Anzahl der Weiterbildungen überfordert oder schaffen ihre tägliche Arbeit nicht mehr, wodurch ihre Zufriedenheit sinkt (s. Abbildung 3). Eine Korrelationsanalyse könnte fälschlicherweise eine schwache oder gar keine Beziehung anzeigen, obwohl tatsächlich ein signifikanter Effekt vorliegt.

Abbildung 3: Fiktives Beispiel. Es besteht ein kurvilinearer Zusammenhang zwischen der Anzahl der Weiterbildung und der Arbeitszufriedenheit (grün Linie). Der lineare Korrelationskoeffizient (rote Linie) zeigt allerdings keinen Zusammenhang an.
Darüber hinaus können sog. Ausreißer die Analyse verzerren, da sie den Koeffizienten künstlich erhöhen oder senken können. Solche Ausreißer müssen also vor der Analyse identifiziert und ggf. ausgeschlossen werden.
Interpretation und Anwendung von Korrelationskoeffizienten
Beachtet man die Voraussetzungen für die Berechnung einer Korrelation und schließt andere Zusammenhangsarten (wie z.B. kurvilineare oder logarithmische) aus, gibt der Korrelationskoeffizient eine klare Aussage darüber, wie stark zwei Variablen zusammenhängen. Wichtig dabei ist jedoch, dass lediglich Zusammenhänge dargestellt werden, keine Kausalitäten. Um dabei Ursachen als solche zu identifizieren, müssen die Variablen zu verschiedenen Zeitpunkten erhoben werden. So könnten Sie zum Beispiel zu einem festen Zeitpunkt feststellen, dass sich die Produktionsfehler in Ihrem Unternehmen erhöhen. Mit Hilfe einer Korrelationsanalyse identifizieren Sie Zusammenhänge zwischen mangelhaften Lieferungen an Rohstoffen und der Anzahl an Produktionsfehlern. Sie wechseln den Lieferanten und erhalten nun wieder qualitativ hochwertige Rohstoffe. Anschließend messen Sie zu einem bestimmten Zeitpunkt nach dem Lieferantenwechsel die Anzahl der Produktionsfehler noch einmal. Ist diese gesunken, bestätigt dies nicht nur den Zusammenhang, sondern lässt eindeutige Schlüsse auf den Zusammenhang zwischen Ursache und Wirkung zu.Ein beliebtes Beispiel in diesem Kontext ist der Zusammenhang zwischen der Anzahl der Störche und der Geburtenrate in einem Dorf. Es besteht tatsächlich oft eine positive Korrelation zwischen diesen beiden Variablen, d.h. je mehr Störche in einem Dorf nisten, umso mehr Kinder werden geboren. Nun werden Sie wissen, dass hier keine Kausalität bestehen kann - schließlich bringt der Storch nachweislich nicht die Kinder. Hierbei handelt es sich um eine sog. Scheinkorrelation - ein Zusammenhang, bei dem die beiden Variablen nicht direkt miteinander zusammenhängen. Bei der Korrelation zwischen Störchen und Geburten wird vermutet, dass eine dritte Variable, die sowohl die Anzahl der Störche als auch die Geburtenrate beeinflusst, für den Zusammenhang verantwortlich ist - nämlich die Ernteerträge. In guten Erntejahren nisten mehr Störche in dem Dorf, da sie mehr Futter finden. Gleichzeitig steigt der Wohlstand, was die Geburtenrate steigert.
Einsatz von Streudiagrammen im Qualitätsmanagement
Bleiben Sie wissbegierig!
Lesen Sie auch:
- Überblick über die sieben wichtigsten Werkzeuge zur Qualitätsverbesserung
- Pareto-Analyse – Priorisierung im Qualitätsmanagement
- Ishikawa-Diagramm – Probleme hinterfragen, Ursachen erkennen
- Fehlersammelliste – Fehler systematisch erfassen
- Das Histogramm – Die Macht der Visualisierung
- Mit der Qualitätsregelkarte Prozesse stabilisieren und Produktqualität erhöhen

Zugehörige Produkte
Qualitätsmethoden - Techniken zur Problemanalyse und Problemlösung
Freie Plätze : 100
Präsenz
|
Live-Webinar





